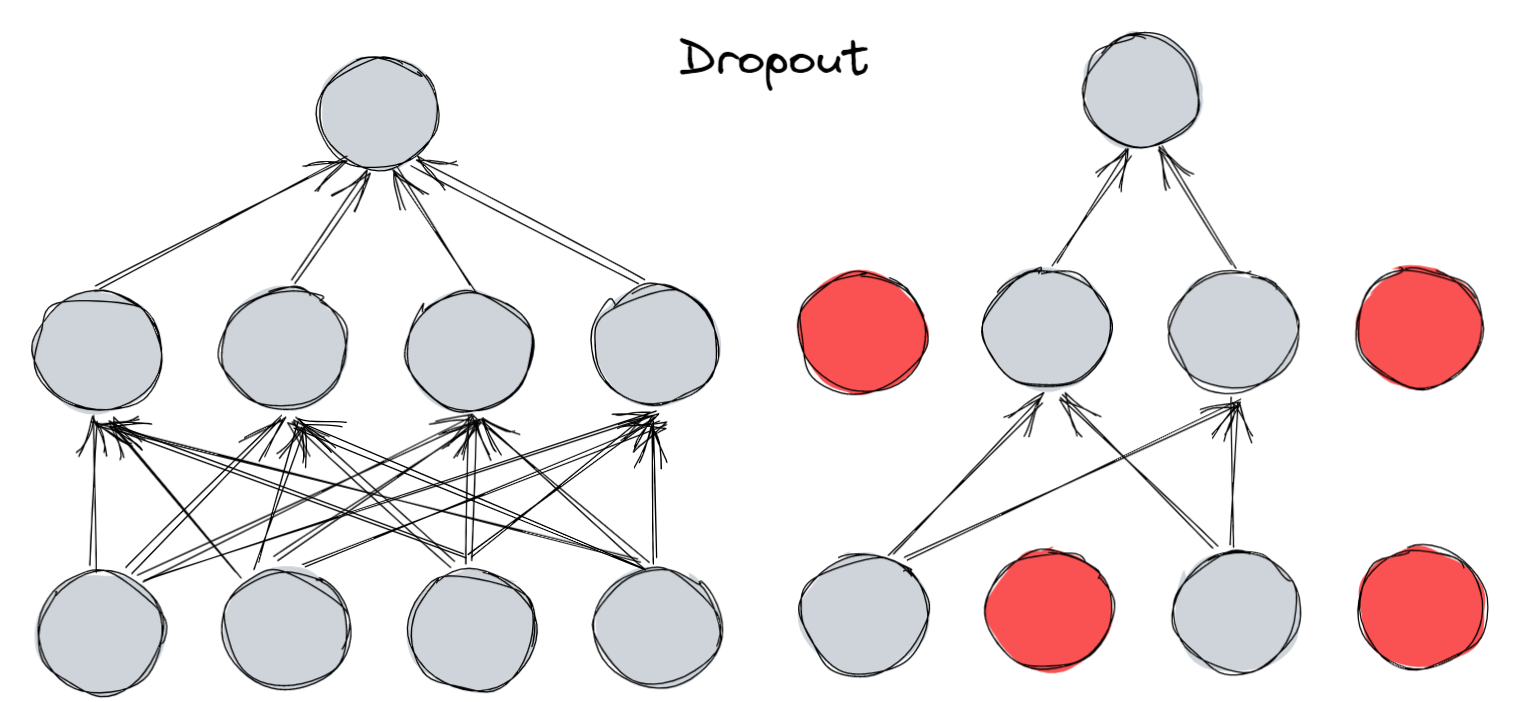
Dropout

Dropout

---

• https://arxiv.org/abs/1207.0580
• https://jmlr.org/papers/v15/srivastava14a.html

Overfitting in NN

---

• layer 마다 L1, L2 regularization을 적용함
• 그러나 이것으로는 부족하다!
  • co-adaptation

co-adaptation

---

• 일부 노드들이 서로 상쇄되면서 아무 일도 안해버림
  • 즉 일부 뉴런들이 의존적으로 변해버림
  • 노드의 낭비와 컴퓨팅 파워, 메모리 낭비를 야기함

dropout

---

• 이를 풀기 위한 새로운 regularization
• 하나의 모델이 다른 여러 모델을 시뮬레이션 하는 결과

Dropout

---

• $z \sim \text{Bern}(p)$
  $$h_i^{(l+1)} = \sigma(\bold w_i^{(l+1)\top}(\bold h^{l}\odot\bold z^l+b_i{(l+1)}))$$
• 0이 곱해지면 노드는 죽어버림
  • 평균적으로 반이 죽음

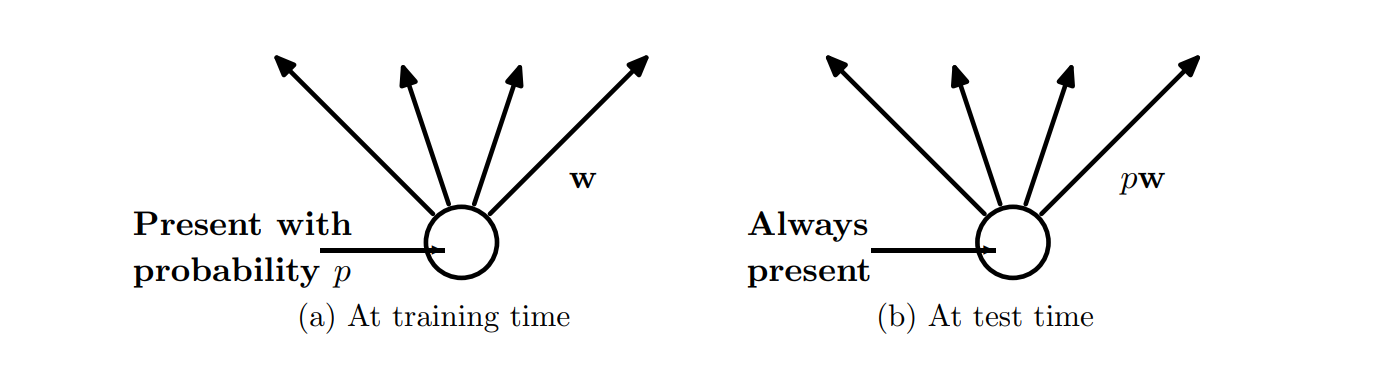
scale down

• 두번째 논문 3페이지 참고
• 훈련 시와 테스트 시 노드 수의 차원이 다른 문제가 있다.
  • 크기 조정이 필요하다.
• 테스트 시에는 drop training을 할 때 사용한 $p$ 값을 가중치에 곱해서 사용한다.

Understanding dropout

---

• 논문 참고

$$\mathcal E_N = {1\over2}(y-\sum_jp_jw_jx_j)^2$$

$$\mathcal E_D = {1\over2}(y-\sum_jz_jw_jx_j)^2$$

• single linear layer with a regular network, dropout network

  • $z \sim \text{Bern}(p)$
  • $p = \mathbb P(z = 1)$

• 그래디언트를 취하면

$${\partial \mathcal E_D\over \partial w_i } = -yz_ix_i + w_iz_i^2x_i^2+\sum_{j\ne i}w_jz_jz_ix_jx_i$$

$${\partial \mathcal E_N\over \partial w_i } = -yp_ix_i + w_ip_i^2x_i^2+\sum_{j\ne i}w_jp_jp_ix_jx_i$$

• 평균을 취하면

$$\mathbb E \left[ {\partial \mathcal E_D\over \partial w_i } \right] = -yp_ix_i + w_ip_i^2x_i^2 + w_i \text{var}(z_i)x_i^2 + \sum_{j\ne i}w_jp_jp_ix_jx_i$$

$$= {\partial \mathcal E_N\over \partial w_i } w_ip_i^2x_i^2 + w_i \text{var}(z_i)x_i^2$$

$$= {\partial \mathcal E_N\over \partial w_i } w_ip_i^2x_i^2 + w_i p_i(1-p_i)x_i^2$$

• 이 식은 regularized network를 최소화한 것과 같다.
  • 즉 아래 식을 미분하면 위의 식이 나옴

$$\mathcal E_R = {1\over2}(y-\sum_jp_jw_jx_j)^2 + {1\over2}\sum_j p_i(1-p_i)w_j^2x_i^2$$

Inverted Dropout

---

• train 에서 dropout을 하고 가중치에 rescale을 진행함
  $$\bold w_i^{(i)} = w_i^{(i)} / \ p$$
• 즉 test에서 scale하지 않음

etc

---

• dropout은 레이어마다 rate 값을 다르게 줄 수 있다.

  • hyper param 이다.

• Fully connected layer에서는 잘 사용하지만

  • cnn에서는 batch normalization이 나오고 잘 안쓰게됨