HyperLogLog 과제

개요

이번 학기에 cmu의 db강의를 따라 들으려 한다. c++ 연습을 위한 과제가 바로 올라왔는데, HyperLogLog를 구현하는 과제이다.

이것도 못 풀면 강의 드랍하라는 것 같다.

과제 나오자마자 풀었는데, test를 계속 틀렸었다. 머리 박고 있었는데, test code의 값이 잘 못 올라와 있던 것이었다.

test 업데이트와 동시에 task2도 추가되었는데, primer의 HLL 구현을 비스무리하게 만드는 것이다. 다만 이번에도 test case 병크를 터트려놔서 머리를 박았다.

구현이 깔끔하지는 않은 것 같다. 배열에 접근할 때 인덱스마다 락을 주면 좋을 거 같은데, 배열이 상당이 커서 mutex 범위를 정해야 할 거 같다. 귀찮아서 업데이트 전체를 mutex로 묶었다.

아래는 HLL과 Presto’s에 관한 meta의 글의 정리이다.

문제 정의

set의 cardinality를 구하는 문제이다. 단순히 해시를 사용할 수 있지만, 이는 다음과 같은 문제가 있다.

• computationally intensive
• demand too much memory

이를 해소하기 위해 정확도를 포기하고, 추정을 한다.

확률을 이용하자

우선 입력되는 값들을 uniform distribution으로 바꿀 필요가 있다. 이를 위해서 hash를 이용한다.

hash의 결과로 bit pattern을 뽑아낸다. 이후 오른쪽으로부터, 0이 연속으로 몇 개 나왔는지 센다. 모든 input에 대해 $p(x_i)$(연속된 0의 개수)을 구하면, cardinality를 $2^{max(p(x_1), p(x_2), … p(x_M))}$ 로 예측할 수 있다.

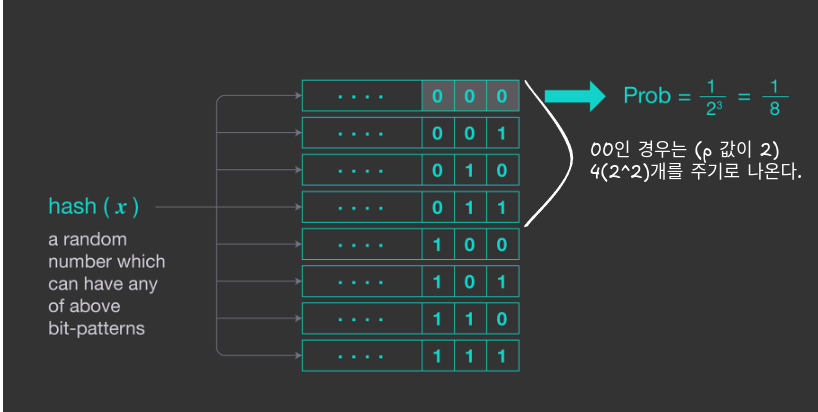
이렇게 예측하는 이유는 직관적으로 설명해보면 다음과 같다. k개의 연속된 0이 나올 확률은 $1/2^k$ 이다. 이상적으로 uniform한 분포면, k개의 연속된 0은 $2^k$개의 distinct entries를 주기로 나오게 된다. 그래서 max연산으로 가장 큰 k를 구하고, $2^k$를 cardinality로 추정하는 것이다.

다만 두 가지 문제점이 존재한다.

1. 추정된 값은 $2^n$이다.
2. 분산이 매우 크다.
   1. 예로 처음 입력의 hash값이 0으로만 이루어진 경우를 생각하자.

하지만 메모리 사용량은 매우 줄어들었다. maximum 값만 유지한다. (연속된 0이 32개까지 일 때, 5비트만 유지하면 된다.)

정확도를 올리자

추정을 여러 번 시도한다. 이후 이들의 평균 값을 구한다.

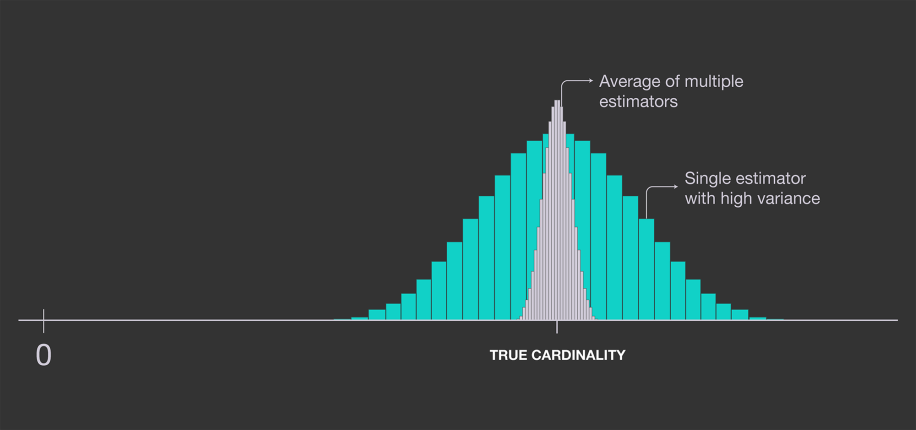
이를 위해 독립된 hash함수가 필요하다. (다른 결과를 뱉어내는) 하지만 이 경우 computationally expensive하다.

Durand and Flajolet 들이 하나의 hash함수만을 이용하는 방법을 제시했다. m개의 독립된 추정을 구하기 위해, m개의 bucket 배열을 만든다.
bit pattern의 앞 부분을 bucket을 indexing하는데 사용한다.

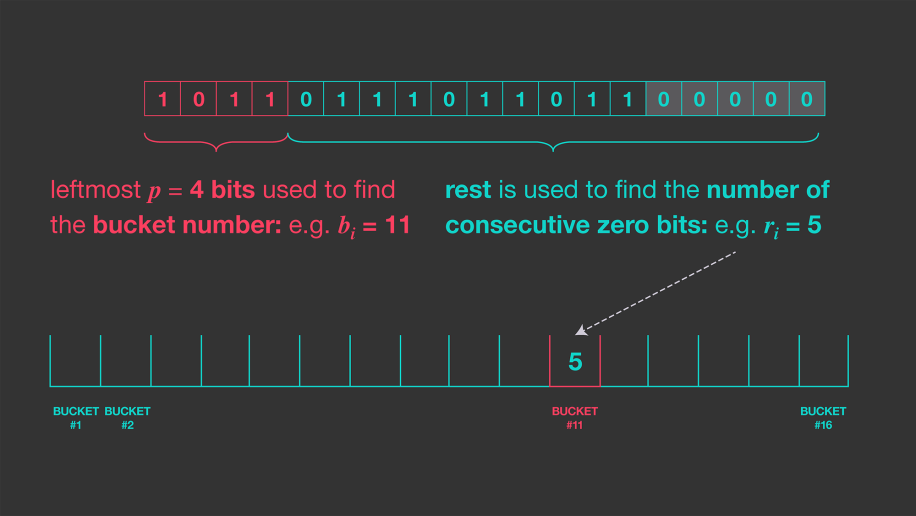
이 방법은 정확도 손실 없이 m개의 hash를 사용할 computing을 줄여준다. 이 절차를 stochastic averaging이라고 한다.

이 부분의 디테일은 논문을 봐야할 것 같다.

다른 방식으로 생각해보면, 큰 값에 민감한데, 이를 평균을 이용해 robust하게 만든다.

위 방법의 cardinality는 다음과 같이 계산된다. \(\mathrm{CARDINALITY_{LogLog}} = \mathrm{constant} \cdot m \cdot 2^{{1\over m}\sum_{j=1}^N{R_j}}\) 통계적 분석에 의하면 값을 크게 추정하는 bias가 있어, constant=0.79402로 두고 사용한다. 이 알고리즘 방식을 LogLog(Durand-Flajolet)라고 부른다. 이때 standard error는 $1.3 \over \sqrt m$ 이다.

m은 bucket의 수

5비트 크기의 bucket을 2048개 사용했을 때, 최대 $2^{27}$개의 ardinalities를 측정할 수 있다. (조정된 값이다.) 사용된 메모리는 2048*5 = 1.2KB이다.

HLL

두 가지의 추가 개선 방법이 있다.

• 작은 70% 값들만 이용하는 방법
• 조화 평균을 이용하는 방법

후자의 방법이 HLL이며, standard error가 $1.04\over \sqrt m$ 까지 줄어든다. \(\mathrm{CARDINALITY_{LogLog}} = \mathrm{constant} \cdot m \cdot {{m\over {\sum_{j=1}^N{2^{-R_j}}}}}\)

presto의 cardinality 구현은 두 가지 layer를 이용한다.

• sparse
  • cardinality가 작다면, 이를 이용해서 계산한다.
  • 정확하게 측정하기 위해, 모두 카운팅한다고 생각하면 된다.
• dense
  • sparse로 작동하다가, 메모리 임계를 넘으면 dense로 변경된다.
  • HLL을 이용한다.

dense에서 HLL을 구현할 때 두 가지 자료구조를 이용한다. bucket과 overflow entries다.

단순히 오른쪽부터 연속된 0의 길이를 구하고, bucket에 저장하면 됐었다. 하지만, presto에서는 bucket 크기에 4비트를 할당했고, 만약 그 이상의 비트를 사용하면 overflow entries에 상위 비트들을 저장한다.

Based on the statistical properties of the HLL algorithm, 4-bits is sufficient to encode the majority of the values in a given HLL structure.

예로 길이가 32라면, bucket 하나의 크기가 4비트이기에, 하위 4비트를 저장한다. 이후 앞의 3비트는 overflow entries에 저장된다.

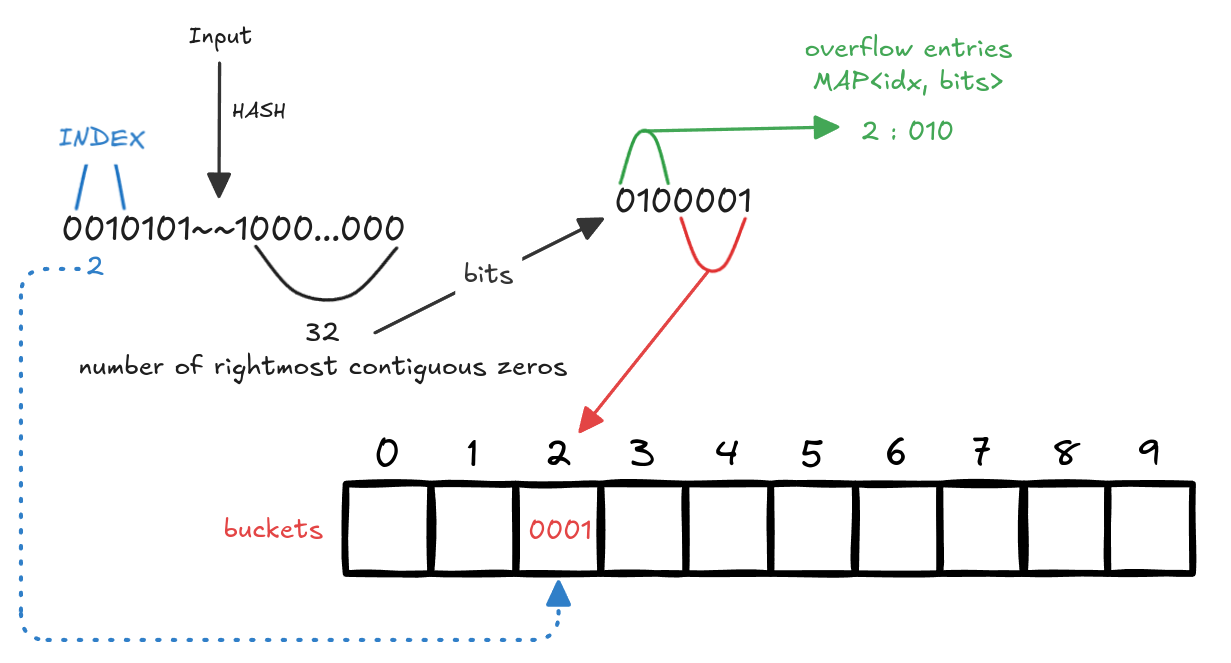
이러면 조금이나 메모리를 더 아낄 수 있다. 주의할 점은 위의 방법은 저장하는 방법이다. 기존의 업데이트 방법이(max)나 비교하는 값은 HLL 그대로이다. 즉 값을 업데이트할 때는 overflow entries와 buckets을 합쳐 복원해야한다.

REF, 읽어볼 글들

메타 글 https://engineering.fb.com/2018/12/13/data-infrastructure/hyperloglog/

위키 https://en.wikipedia.org/wiki/Flajolet%E2%80%93Martin_algorithm https://en.wikipedia.org/wiki/HyperLogLog

논문 https://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf

영상 https://www.youtube.com/watch?v=lJYufx0bfpw https://en.wikipedia.org/wiki/HyperLogLog