Normalization
종류
- Batch normalization
- Layer normalization
- https://arxiv.org/pdf/1607.06450.pdf
- RNN, Transformer
- Instance normalization
- Group normalization
Normalization
- Standardization 표준화
- 왜 할까?
- 범위가 너무 넓어 step size를 정하기 어렵다.
- 보수적으로 잡게 됨
- 범위가 너무 넓어 step size를 정하기 어렵다.
- 방법
- 평균이 0, 분산이 1이도록 만든다.
Batch Normalization
- data들이 whitened하면 Training converges 가 빠르게 진행된다.
whitened : zero mean, unit variance, decorrelated
- Deep Neural Networks 에 적용을 해보자!
Internal Covariate Shift
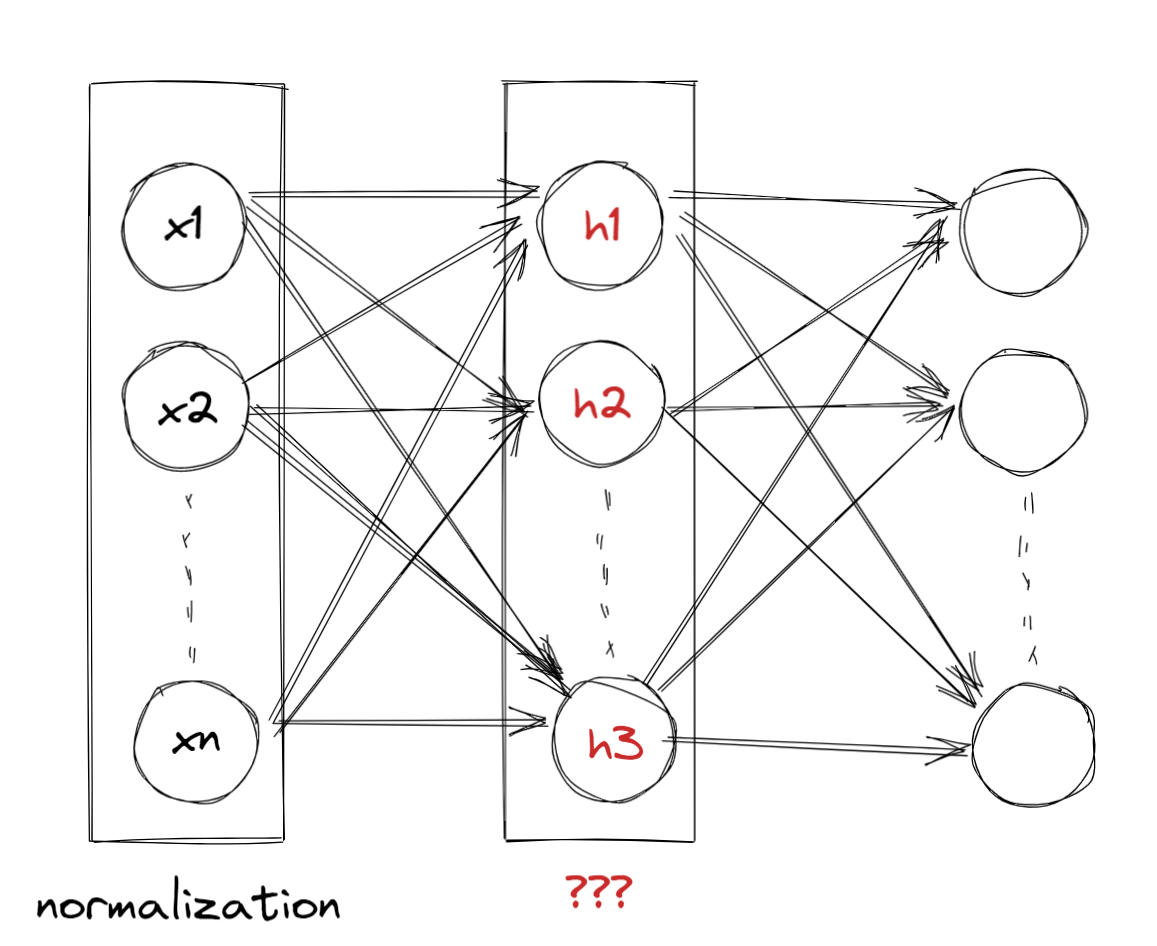
- 처음 input은 표준화 되어있다.
- 그러나 다음 layer에서는 표준화 되어 있지 않다.
- 보통 input distrubution 이 input과 output에서 같다고 생각한다.
- 만약 다른 상황이라면 이를 Covariate shift라고 부른다.
- 지금은 layer에서 벌어진 상황이기에 Internal Covariate shift라고 부른다.
Batch Normalization
- 이제 batch normalization에 대해 알아보자.
- 우선 하나의 노드를 기준으로 생각한다.
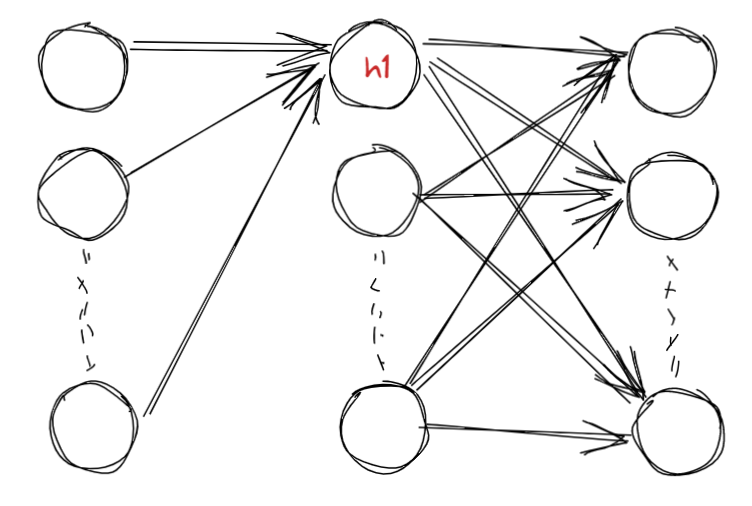
batch는 입력 데이터의 개수이다.
- 입력 노드의 수가 아니다.
batch가 10이라면 10번 feed foward가 발생한다.
- 이때 h1이 된 값은 10개가 존재한다.
- 이 값들을 가지고 normalization을 진행한다.
일때 수식으로 정리해보면 다음과 같다.
이후에는 Scale 과 Shift 과정을 지난다.
- 이는 하나의 layer가 추가된 것으로 볼 수 있다.
- 이는 하나의 layer가 추가된 것으로 볼 수 있다.
왜 scale과 shift 과정이 필요할까?
- 다음 그림을 보며 이해해보자.
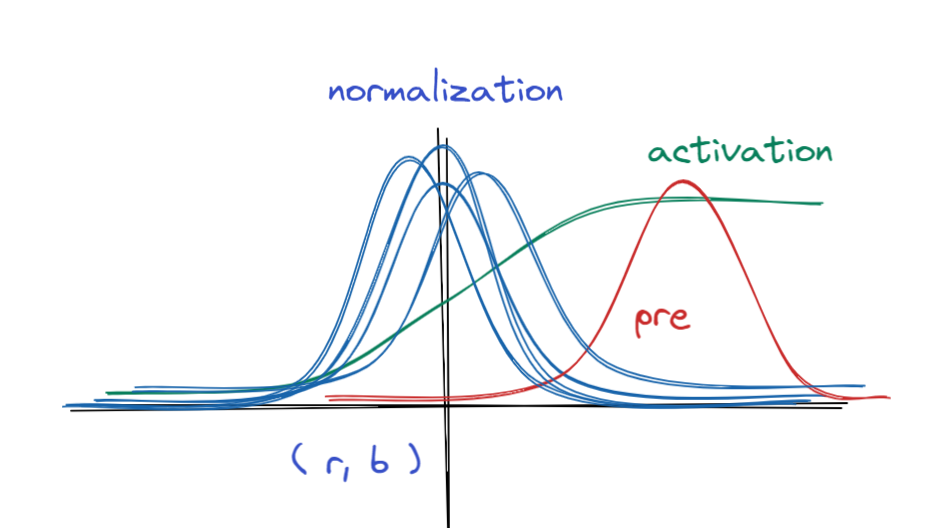
우선 normalization 과정은 빨간 분포를 중앙의 파란 분포로 바꾸는 과정이다.
- 이후 우리는 sigmoid 를 취하게 되는데 빨간색에 위치한 sigmoid의 경사는 파란색 분포보다 완만하다.
- 만약 빨간색에서 계속 기울기가 계산된다면 매우 느리게 converge 할 것이다.
- gradient vanishing 문제
이때 표준화 과정에서 항상 평균을 0으로 분산을 1로 하는 것이 의미가 있을까?
- 우선 표준화 과정의 장점은 빠른 converge이다.
- gradient vanishing 해결
- 하지만 모두 같은 기울기를 가지게 되고 , 이는 활성화 함수가 비선형 함수로써 의미가 없어지게 만든다.
그래서 두 개의 변수를 추가해서 scale과 shift 과정을 만든다.
- 랜덤성을 부여하는 것이다.
- 중앙이 답이 아닐 수도 있으니까
- 두 변수는 역전파 과정에서 학습된다. 즉 데이터가 정한다.
- 랜덤성을 부여하는 것이다.
BN in Inference phase
학습 시에는 배치 크기 기준으로 학습을 했다.
그렇다면 테스트 시에는 무엇을 기준으로 해야 될까?
- 이때는 단순히 마지막 결과를 사용하는 것이 아닌 평균을 이용한다.
즉 한번 배치를 돌 때마다 평균 값과 분산 값이 나오게 됨
- 이 값들을 다시 평균 내서 입력 값을 표준화 하는데 사용한다.
- 이후 학습된 값을 이용해 scale, shift 해준다.
분산을 평균 낼 때는 을 곱한다. (편향)
moving avg를 구한다.
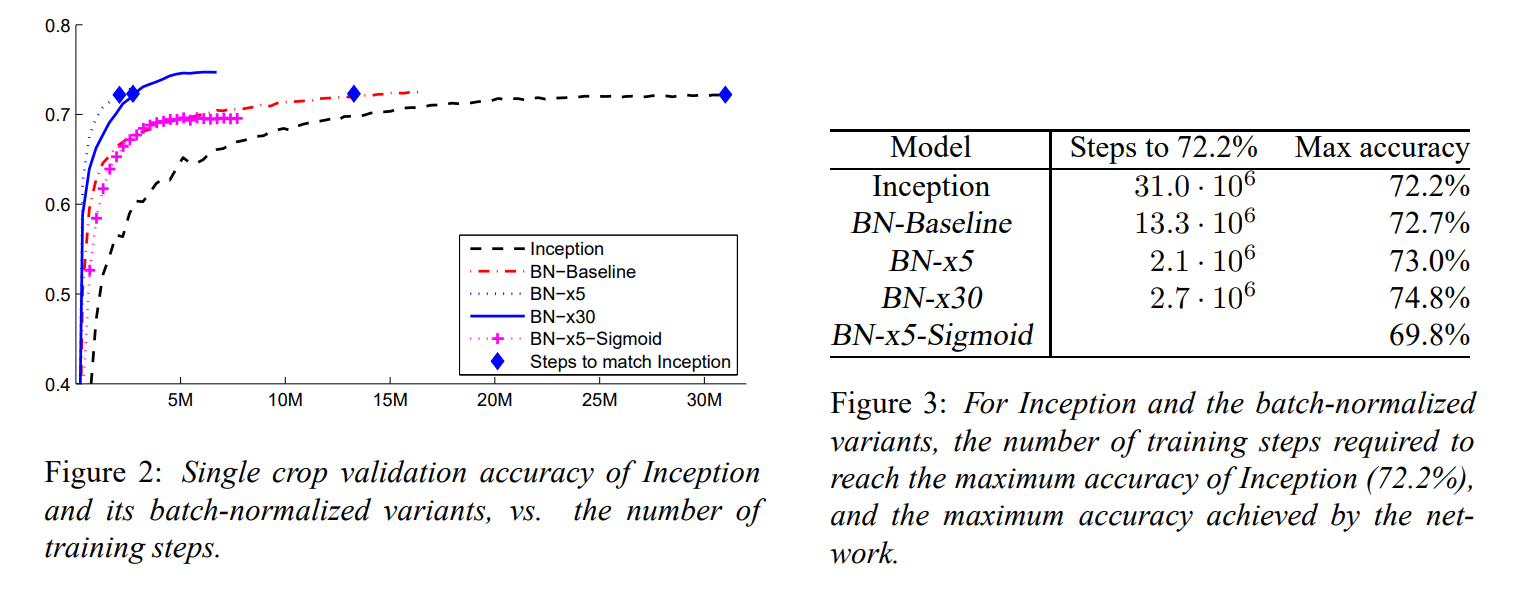
장점
- step size 를 증가시킬 수 있다.
- speed up
- remove dropout
- reduce L2 weight regularization
Layer Normalization
- rnn에는 BN이 잘 안 맞음
- 시간의 흐름이 중요한데 배치마다 평균 내버림
- 배치 사이즈가 작으면 BN의 문제가 있다.
- ( 이유는 찾아보자 )
LN
- average of node
- 말 그대로 레이어 값들의 통계량을 이용한다.
- BN은 Batch를 기준으로 통계량을 만들어 이용했다면
- LN은 한 input에 대하여 작동하며, 같은 층의 노드들의 통계량을 사용한다.
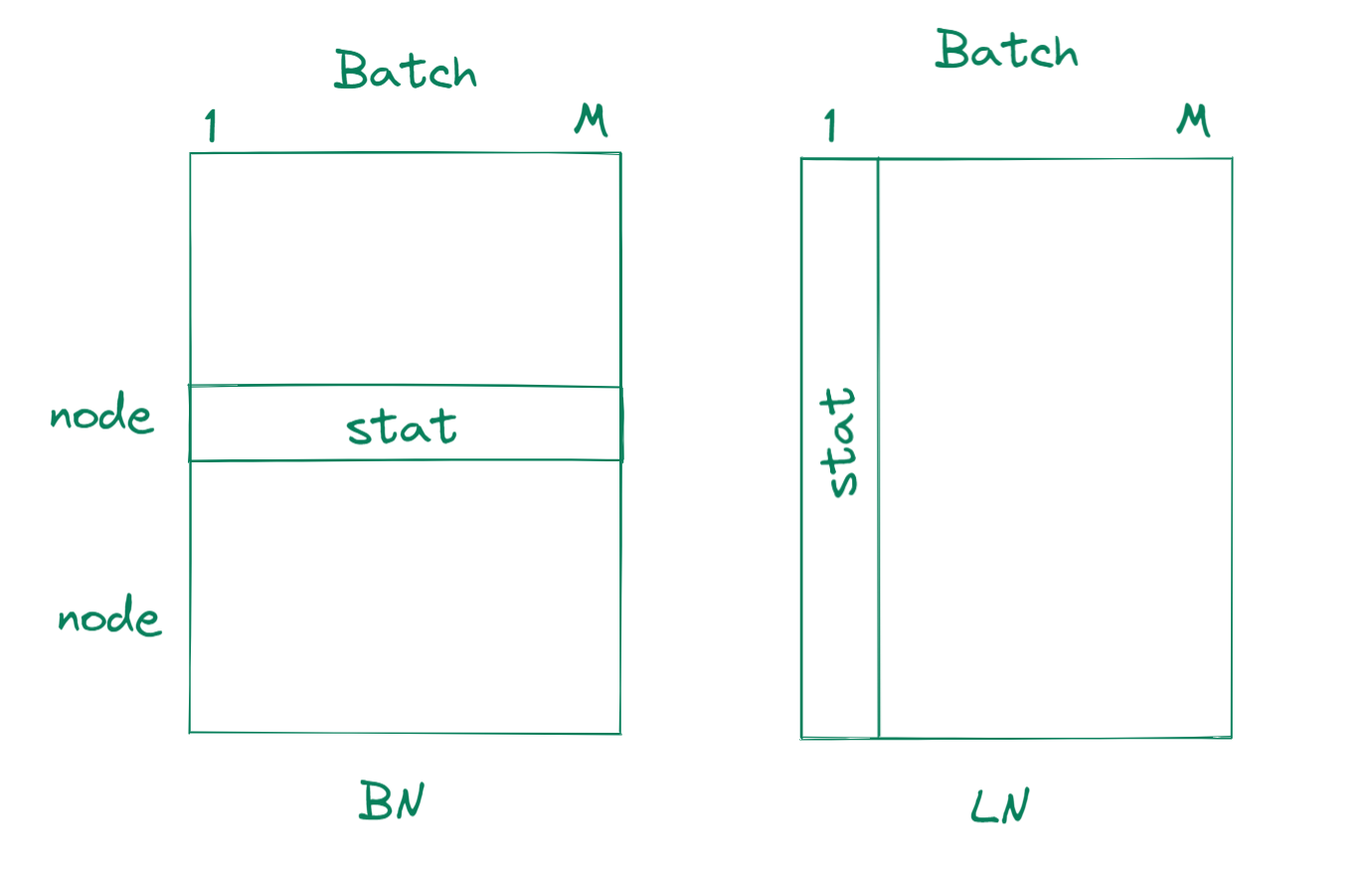
- 다음과 같은 결과가 나온다.
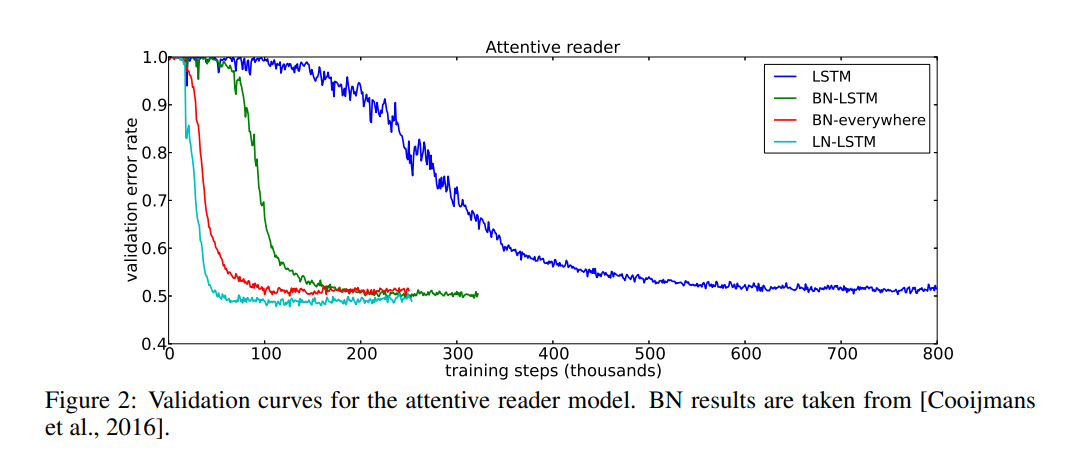
이후 내용
- CNN을 배우고 오자!