Backpropagation

Backpropagation

---

Gradient Descent

---

• 최적화 기법에서 가장 기본적이고 중요한 방법이다.

  • 제약 조건이 없는 convex, differentiable한 함수의 최적화 문제의 해결책이다.

• 기준을 만족할 때까지 다음 식을 반복한다.
  $$x^{k+1} = x^{k} - t_k\nabla f(x^k)$$

$f$는 error function이다.

문제점

---

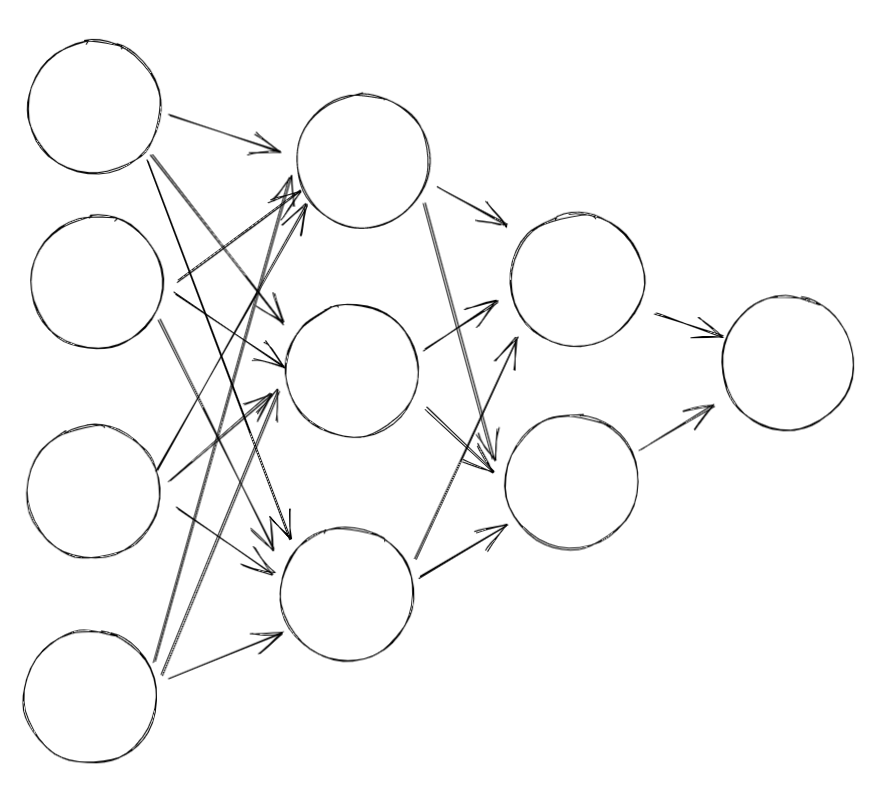
• 출력 층과 바로 그 전 은닉층은 직접적인 관계가 있다.

• 하지만 다른 은닉층들의 $w$값과의 관계는 쉽게 구할 수 없다.

  • 즉 업데이트를 하기 어렵다.

• 많은 연구자들은 다층 퍼셉트론을 훈련할 방법을 찾기위해 오랫동안 연구했다. 그러나 성공하지 못했다.

• 1986년 루멜하트, 힌턴, 윌리엄스가 역전파 훈련 알고리즘을 소개했다.

  • 1985 Learning internal Representations by Error Propagation
  • 1986 Learning representations by back-propagating errors / nature

자동 미분 : 자동으로 그레디언트를 계산하는 것
역전파에서는 후진 모드 자동 미분을 사용한다.
이는 미분할 함수가 변수가 많고 출력이 적은 경우 잘 맞는다.

Backpropagation

---

• 알고리즘은 간단하다.

1. 정방향 계산을 한다.
   • forward pass
2. 오차 측정 값을 구한다.
3. 각 출력 연결이 오차에 기여하는 정도를 계산한다. (역방향 계산)
   • 연쇄 법칙이 이용된다.
4. 모든 연결 가중치에 대한 오차 그레디언트를 구하면 모든 연결 가중치를 업데이트한다. ( 경사 하강법 )

역방향 계산

---

• 각 가중치들이 오차 값에 영향을 미치는 정도를 구하기 위해서는 변화율을 구하면 된다.

$$\partial E\over \partial w_n$$

• 하지만 출력 층으로부터 멀리 떨어진 가중치의 오차 함수에 대한 변화율을 구하기는 어렵다.

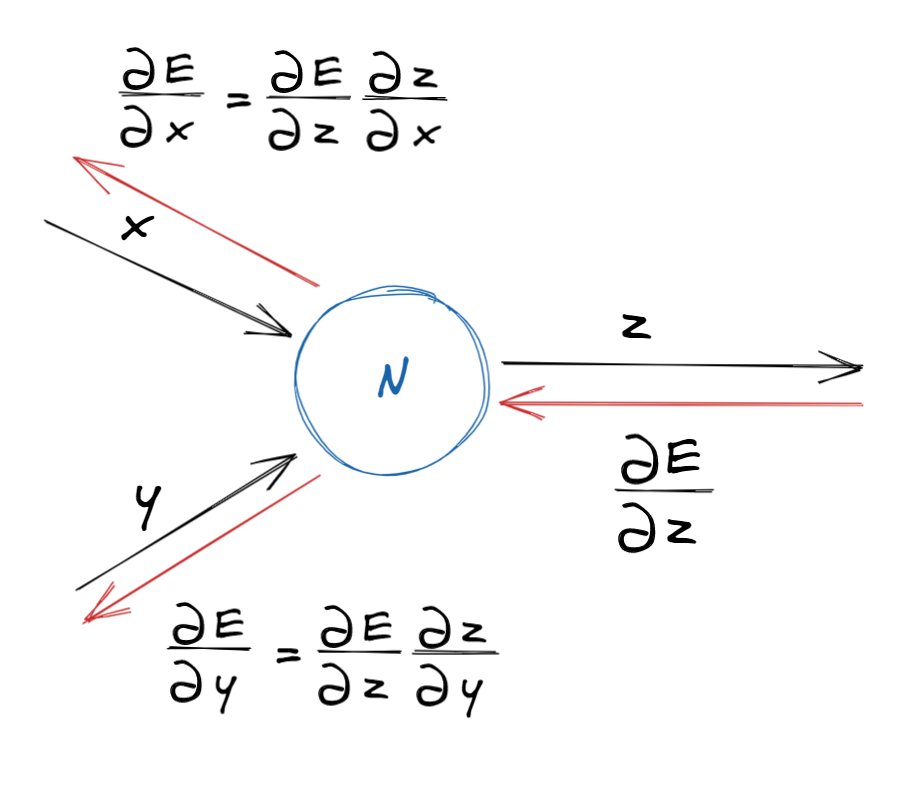
• 이를 해결하는 방법은 연쇄법칙이다.
  • 돌아오면서 뒤로 전해진 변화율에 해당 노드에서의 변화율을 곱해주면 된다.

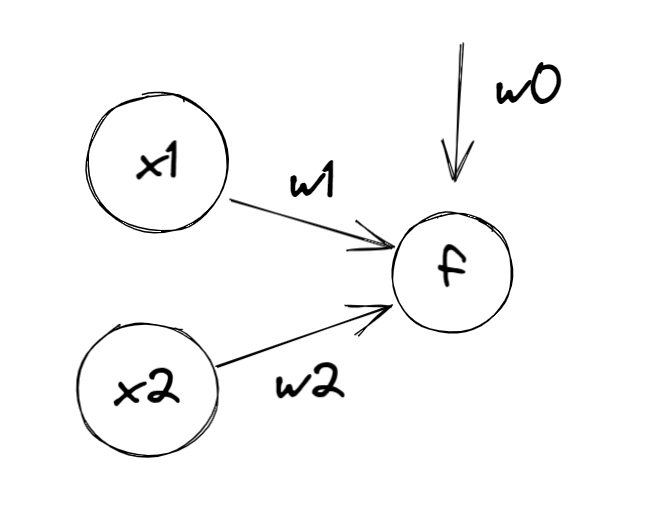
• 이를 그래프를 이용해 적용해보자.

Computational Graphs

---

• 다음과 같은 상황의 역방향 계산을 진행해보자.

$$f(w,x) = {1\over1+e^{-(w_1x_1+w_2x_2+w_0)}}$$

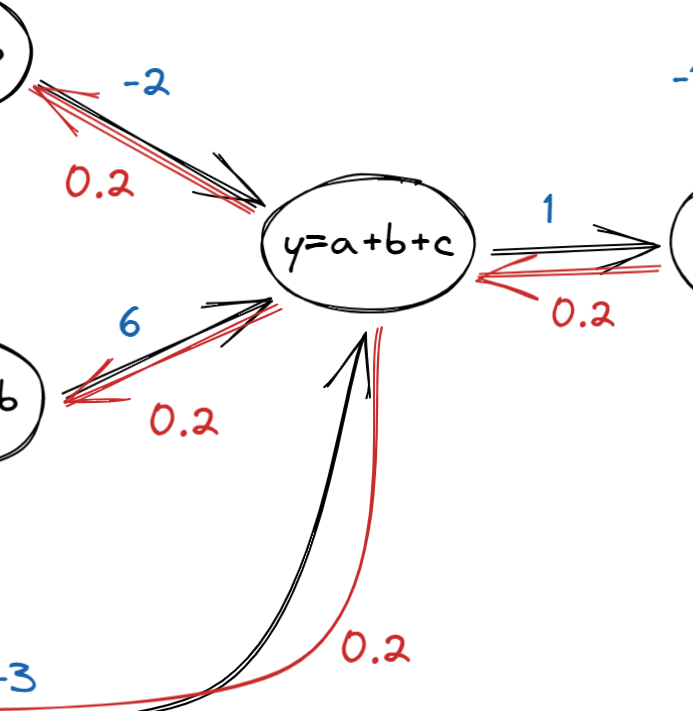
• 다음과 같이 계산 할 수 있다.
  • 파랑 -> 정방향
  • 빨강 -> 역방향

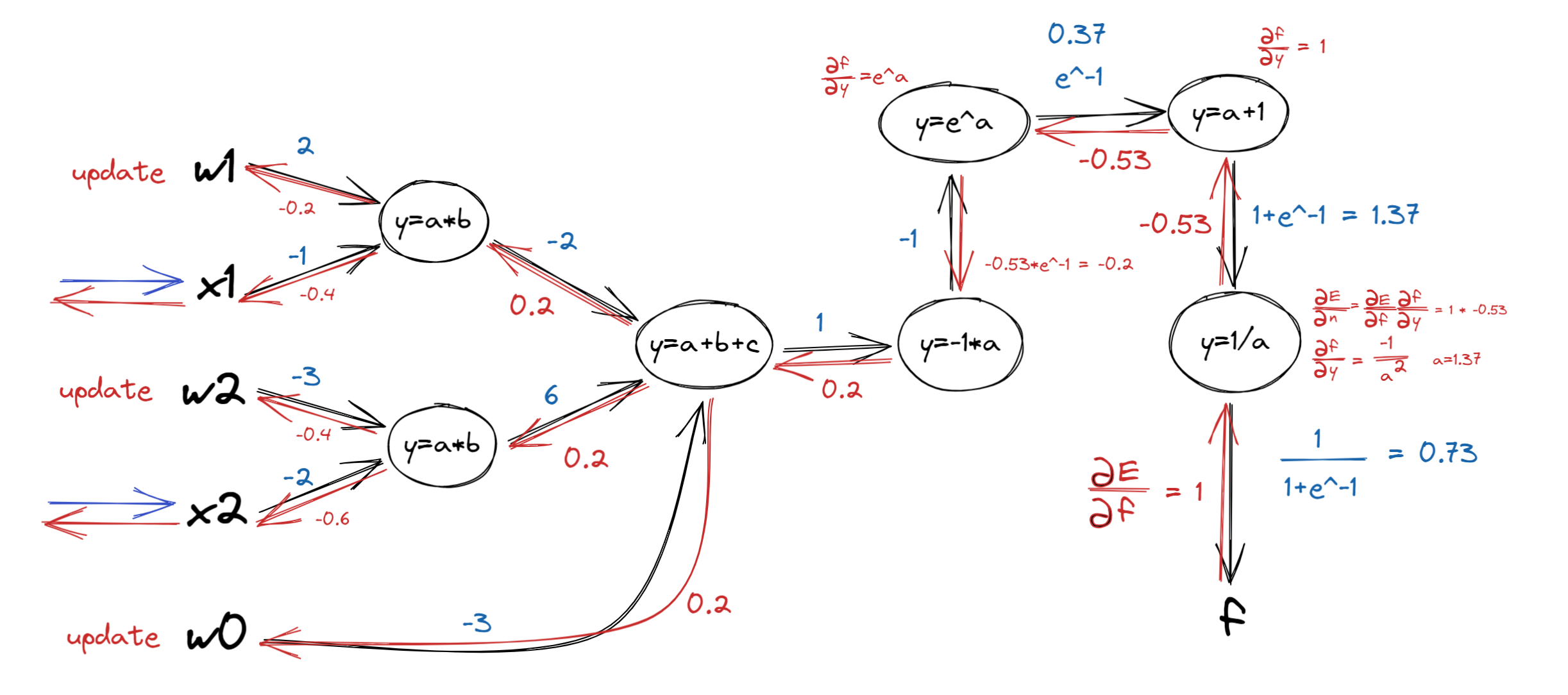
• 곱셈 관계에서는 역방향 계산시 가중치를 바꿔서 곱해준다.

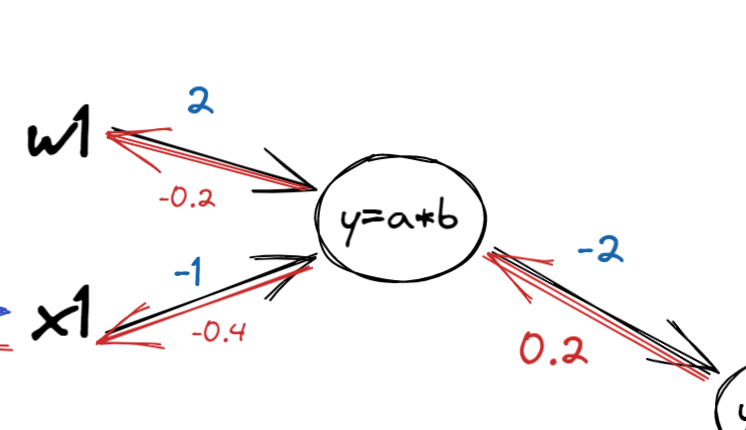
• 단순 덧셈은 그대로 지나간다.
  

• 나머지는 차근하게 미분을 해보면 이해할 수 있다.

• 만약 x1노드가 다른 노드에도 연결되었다면, 값은 들어온 값들의 평균으로 정해진다.

  • 참고 https://www.youtube.com/watch?v=tIeHLnjs5U8

Application

---

• 핸즈온 머신러닝 2판 p.366 설명 참고

회귀 MLP의 전형적인 구조

---

하이퍼 파라미터	일반적인 값
입력 뉴런 수	특성마다 하나
은닉층 수	문제에 따라 다름, 일반적으로 1~5사이
은닉층의 뉴런 수	문제에 따라 다름, 일반적으로 10에서 100사이
출력 뉴런 수	예측 차원마다 하나
은닉층의 활성화 함수	ReLU 또는 SeLU
출력층의 활성화 함수	없음, 양수이면 ReLU/sorfplus, 범위 제한 목적이면 Logistic/tanh
손실 함수	MSE, 이상치 있다면 MAE, Huber

분류 MLP의 전형적인 구조

---

하이퍼파라미터	이진분류	다중 레이블 분류	다중 분류
입력층과 은닉층	회귀와 동일	회귀와 동일	회귀와 동일
출력 뉴런 수	1개	레이블마다 1개	클래스마다 1개
출력층의 활성화 함수	로지스틱 함수	로지스틱 함수	소프트맥스 함수
손실 함수	크로스 엔트로피	크로스 엔트로피	크로스 엔트로피