Home Optimization
Post
Cancel

Optimization

Posted Jul 14, 2022
By baekbumsung
8 min read

Problem

  • 목적은 loss, error function을 최소화하는 θ\theta값을 구하는 것이다.

Gradient Descent

간단한 정리

역전파에서 간단히 다루었다.

  • 최적화 기법에서 가장 기본적이고 중요한 방법이다.

    • 제약 조건이 없는 convex, differentiable한 함수의 최적화 문제의 해결책이다.

  • 기준을 만족할 때까지 다음 식을 반복한다.
    xk+1=xk−tk∇f(xk) x^{k+1} = x^{k} - t_k\nabla f(x^k)

ff는 error function이다.

Interpretation

모두를 위한 컨벡스 최적화 참고

  • gradient descent는 함수를 2차 식으로 근사한 뒤, 그 함수의 최소 위치를 다음 위치로 선택하는 방법이다.

  • ff를 2차 Taylor로 전개한다.
    f(y)≈f(x)+∇f(x)⊤(y−x)+12∇2f(x)∣∣y−x∣∣22 f(y) \approx f(x) + \nabla f(x)^\top(y-x)+{1\over2}\nabla^2f(x) ||y-x||_2^2

  • 헤시안을 1t1\over t로 대체한다.

    • t = step size

f(y)≈f(x)+∇f(x)⊤(y−x)+12t∣∣y−x∣∣22 f(y) \approx f(x) + \nabla f(x)^\top(y-x)+{1\over2t}||y-x||_2^2

  • 이때 12t∣∣y−x∣∣22{1\over2t}||y-x||_2^2 항은 x 에 대한 proximity term 이다.
    • 앞 식은 선형 근사로 볼 수 있다.

proximity term은 얼마나 가까운가를 나타낸다.
즉 현재 x 에서 크게 벗어나지 않도록 제한한다.

  • 이 식의 최소 값을 구한다. 이는 다음의 x값이 된다.
    xk+1=arg min⁡yf(xk)+∇f(xk)⊤(y−xk)+12t∣∣y−xk∣∣22 x^{k+1} = \argmin_y f(x^k) + \nabla f(x^k)^\top(y-x^k)+{1\over2t}||y-x^k||_2^2

Stochastic Gradient Descent

  • 앞선 gradient descent방법으로 이야기해보자.
  • 에러 함수는 오차의 합으로 구성된 함수의 합이다.
  • 이를 gradient descent로 풀어내려면 함수들의 gradient를 합산하여 구한다.
  • 이후 업데이트한다.

모두를 위한 컨벡스 최적화 참고

x(k)=x(k−1)−tk⋅∑i=1m∇fi(x(k−1)), k=1,2,3,… x^{(k)} = x^{(k-1)} - t_k \cdot \sum_{i=1}^{m} \nabla f_i (x^{(k-1)}), \, k=1,2,3,\dots

  • 그러나 이 방법에는 문제점이 있다.
    • 모든 데이터를 가지고 gradient를 구하는 것은 문제가 된다.
    • 요즘에는 거대한 데이터를 인풋으로 사용한다. 메모리에 올라가기도 힘들다.
    • 즉 계산 오버헤드가 크게 증가한다.

gradient descent를 batch update라고 부른다.

  • 이를 해결하기 위해 다음과 같은 방식이 제안된다.

Mini-Batch gradient descent

  • 이름 그대로 스텝이 진행될 때 모든 배치를 사용하지 않는다.
  • 두가지 방법으로 나눌 수 있다.
  1. mini-batch
    • 작은 개수의 샘플을 이용한다. ( 128, 256 …)
  2. stochastic gradient
    • 1개의 샘플만 이용한다.

사실상 크게 이름을 구분하지 않고 혼용해서 쓴다.

https://towardsdatascience.com/gradient-descent-algorithm-and-its-variants-10f652806a3

Challenges

  • step size를 결정하는데 어려움이 있다.
    • 작다면 너무 느려진다.
    • 크다면 빠르나 끝에 가서 크게 요동친다.
      • fluctuation in the object function
  • learning rate를 스케줄 한다.
    • 처음에는 크게, 나중에는 작게
  • local minima 나 saddle points에 걸리면 나오기 힘들다.

Exponentially Weighted Moving Average

기본 식

  • 전 스텝의 값과 새로운 값의 convex sum이다.
    vt=βvt−1+(1−β)θt \bold v_t = \beta \bold v_{t-1} + (1-\beta) \theta_t
  • β\beta 는 하이퍼 파라미터 (0 ~ 1)
  • vt−1\bold v_{t-1}은 이전 Moving average
  • θ\theta는 현재 구해진 값

정리

  • v0\bold v_0부터 진행해보자.
    v1=βv0+(1−β)θ1=(1−β)θ1 \bold v_1 = \beta \bold v_{0} + (1-\beta) \theta_1 \\ = (1-\beta) \theta_1

v2=βv1+(1−β)θ2=β(1−β)+(1−β)θ2=(1−β)(βθ1+θ2) \bold v_2 = \beta \bold v_{1} + (1-\beta) \theta_2 \\ = \beta (1-\beta) + (1-\beta) \theta_2 \\ = (1-\beta)(\beta \theta_1+\theta_2)

  • 계속 진행하면 다음과 같은 식으로 정리 가능하다.
    vt=(1−β)(βt−1θ1+βt−2θ1+⋯+θt) \bold v_t = (1-\beta)(\beta ^{t-1}\theta_1 +\beta ^{t-2}\theta_1 + \cdots + \theta_t )
  • 11−β1\over{1-\beta} 개의 샘플을 이용한 평균의 근사 값이다.
  • 오래된 데이터는 제곱 값이 매우 작아져 값이 빠르게 작아진다.
    • Exponential decay

Bias Correction

  • 초기 값이 0부터 시작되어 bias가 발생한다.
  • vt1−βt\bold v_t \over 1-\beta^t를 vt\bold v_t대신 사용한다.

자세한 설명 참고

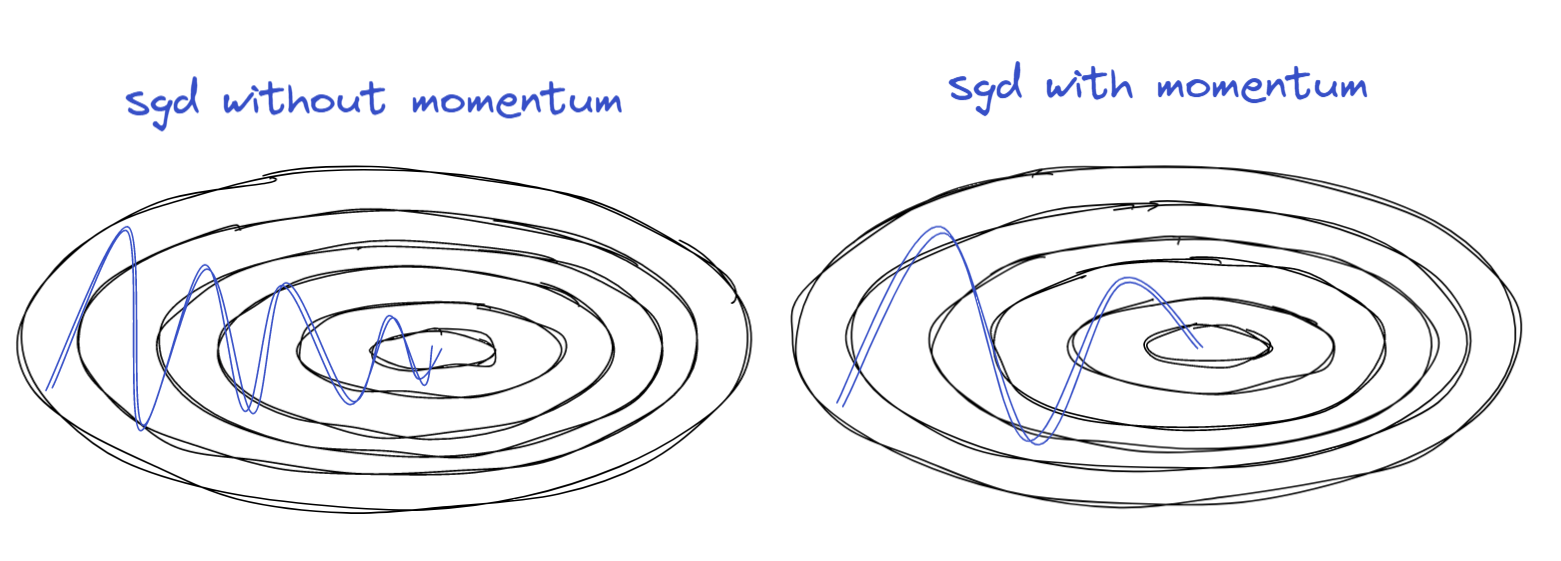
  • 이 방법을 gradient descent에 적용한 것이 모멘텀이다.

Momentum

  • gradient의 moving avg를 이용해서 업데이트함
    vt+1=βvt+(1−β)[∇J(θt)] \bold v_{t+1} = \beta \bold v_t + (1-\beta)[\nabla \mathcal J(\theta_t)]

θt+1=θt−αvt+1 \theta_{t+1} = \theta_t - \alpha\bold v_{t+1}

  • 이전 세대의 gradient값이 같은 방향을 계속 가르키면 가속화된다.

장점

  • 모멘텀 최적화가 경사 하강법보다 빠르다.
  • 빠르게 평편한 지역을 탈출하게 만든다.
  • 지역 최적점을 건너 뛰는데 효과가 있다.
    • 안정되기 전까지 모멘텀 때문에 진동을 하기 때문이다.

핸즈온 머신러닝 p.436

RMSProp

  • gradient 값의 제곱에 moving avg를 적용함
  • RMSProp = Rprop + SGD
  • adaptive individual learning rate for each weight

algorithm

rt+1=βrt+(1−β)[∇J(θt)]2    (element-wise square) \bold r_{t+1} = \beta \bold r_t + (1-\beta)[\nabla \mathcal J(\theta_t)]^2 \ \ \ \ \text{(element-wise square)}

vt+1=∇J(θt)rt+1+ε    (element-wise division) \bold v_{t+1} = {\nabla \mathcal J(\theta_t) \over \sqrt{ \bold r_{t+1}+\varepsilon}} \ \ \ \ \text{(element-wise division)}

θt+1=θt−αvt+1 \theta_{t+1} = \theta_t - \alpha\bold v_{t+1}

  • 만약에 gradient 값이 크면, 그만큼 나눠져서 값이 작아짐
    • learning rate 값이 낮아지는 효과

정리

  • 지수 가중 평균을 이용 -> 경향성 반영
  • 루트로 나누어 학습에 제약을 둠 -> adaptive learning rate
    • 불필요한 진동 감소 및 Gradient Exploding 막음

ADAM

  • ADAM = momentum + bias correction + RMSProp
    • adaptive 스텝 사이즈, 크기

algorithm

vt+1=βvt+(1−β)[∇J(θt)] \bold v_{t+1} = \beta \bold v_t + (1-\beta)[\nabla \mathcal J(\theta_t)]

rt+1=βrt+(1−β)[∇J(θt)]2    (element-wise square) \bold r_{t+1} = \beta \bold r_t + (1-\beta)[\nabla \mathcal J(\theta_t)]^2 \ \ \ \ \text{(element-wise square)}

vtbc=t1−β1t    (bias correction) \bold v_t^{bc} = {\bold t \over 1-\beta_1^t} \ \ \ \ \text{(bias correction)}

rtbc=r1−β2t    (bias correction) \bold r_t^{bc} = {\bold r \over 1-\beta_2^t} \ \ \ \ \text{(bias correction)}

θt+1=θt−αvtbcrtbc \theta_{t+1} = \theta_{t} - \alpha{\bold v_t^{bc} \over \sqrt{\bold r_t^{bc}}}

  • 여기서 αrtbc\alpha \over \sqrt{\bold r_t^{bc}} 값이 adaptive learning rate이다.
    • α\alpha 값은 상수

정리

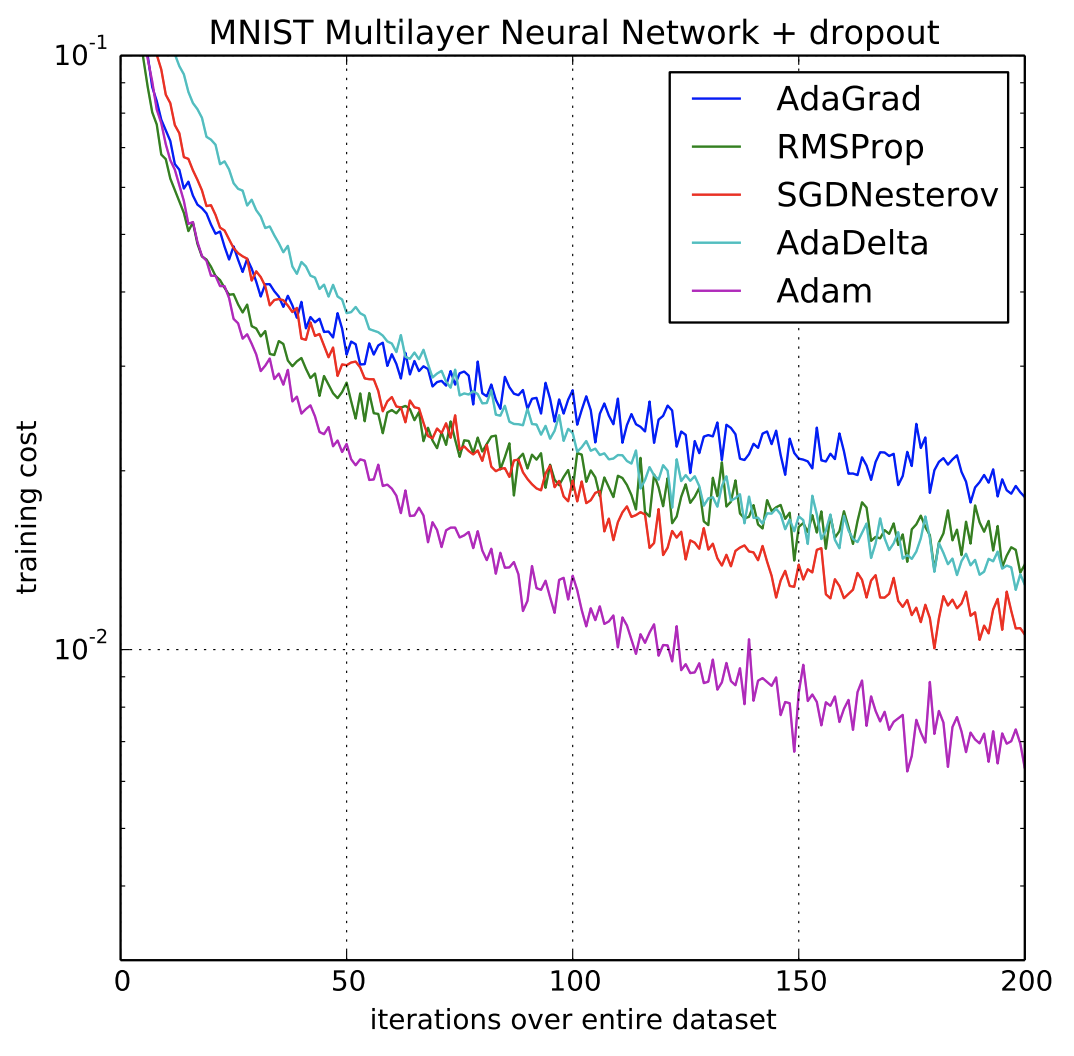
  • adam은 가장 많이 사용되고 있는 옵티마이저이다.
  • 성능 또한 좋다.
    • 하이퍼 파라미터 지정에 대한 부담이 적다. -> adaptive 특성

  • 중간 중간 빠진 옵티마이저는 다음 그림을 통해 살펴보자.

Learning Rate Decay

  • step size를 step마다 줄여줌
  • 1 epoch는 한번 학습된 것이다. ( batch라면 전체 데이터를 한번 트레이닝함 )
  • μ\mu = decay rate, Ω\Omega =epoch num

여러 방법들

α=11+μΩα0 \alpha = {1\over1+\mu\Omega}\alpha_0

α=0.95Ωα0 \alpha = 0.95^\Omega\alpha_0

α=kΩα0 \alpha ={ k\over \sqrt{\Omega}}\alpha_0

α=ktα0 \alpha ={ k\over \sqrt{t}}\alpha_0

CS, AI
cs AI ML summer
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents