Perceptron

Artificial Neuron

---

• 매컬러와 피츠가 제안한 매우 단순한 신경망 모델
• 입력이 일정 개수만큼 활성화되면 출력을 내보냄
• 논문에서 어떤 논리 명제도 계산할 수 있다는 것을 증명함
• MCP뉴런이라 부른다.

뉴런은 행렬 계산의 일부이다. 특별하거나 심오한걸로 생각하지 말자.

Perceptron

---

• 1957년 로젠블라트(Frank Rosenblatt)가 제안
  • TLU : threshold logic unit, LTU : linear threshold unit이라 불리는 형태의 인공 뉴런 기반
  • 입력과 출력이 이진이 아닌 숫자이다.

작동 과정

---

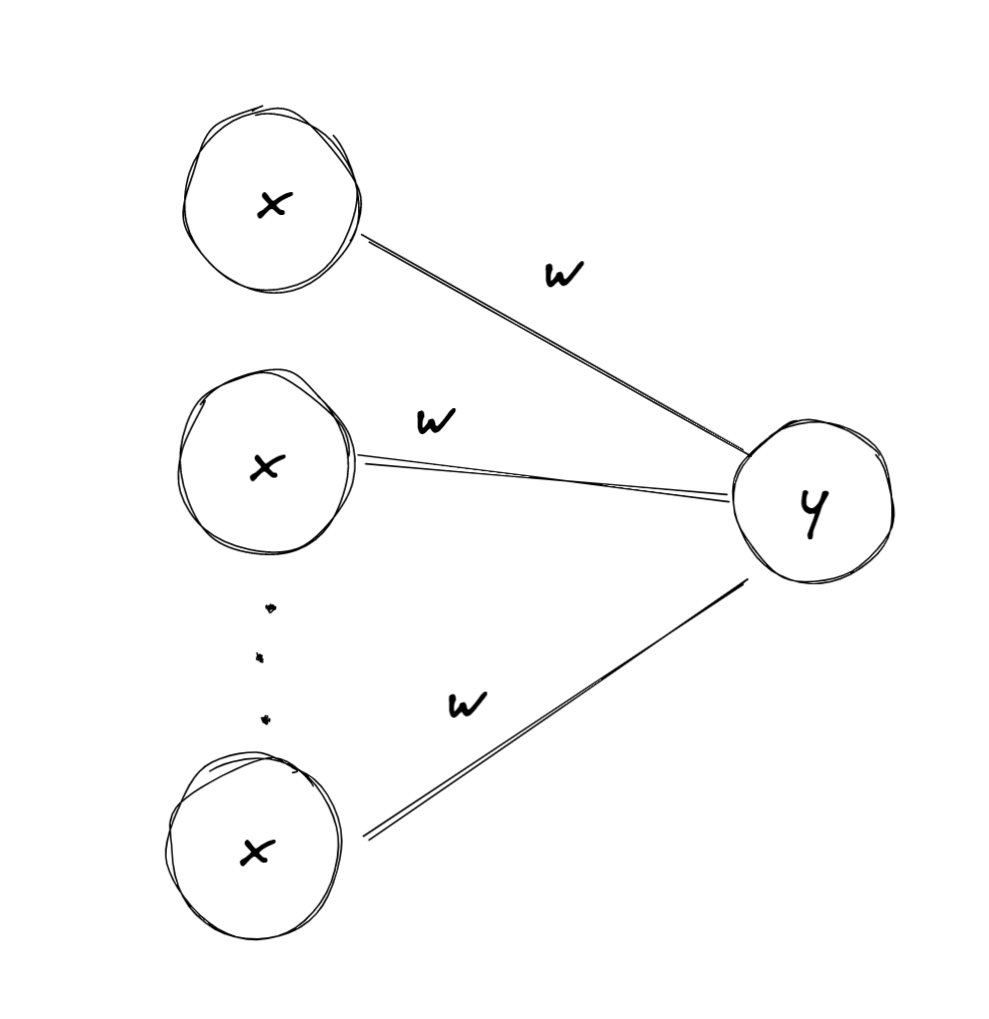
1. 입력의 가중치 합을 계산
   • $z = w_1 x_1+w_2x_2+ \dots+ w_nx_n =\bold w^\top \bold x$
2. 계단 함수 ( step function )을 적용
   • 헤비사이드 계단 함수
     $$\text{heaviside}(z) =\begin{cases} 0 & z < 0\\ 1 & z \ge 0 \end{cases}$$
   • 부호 함수
     $$\text{sgn(z)} = \begin{cases} -1 & z < 0 \\ 0 & z = 0 \\ +1 & z > 0 \end{cases}$$
3. 출력

계단 함수는 TLU인 경우의 활성화 함수이다 .

• 행렬을 이용한 수식 계산
  $$y = \phi(\bold w^\top\bold x + b )$$

$\phi$는 활성화 함수

Linearly Separable

---

• 선형적으로 분류가 가능한 패턴은 linear hyperplane을 통해 나누어질 수 있다.
• 로젠블라트는 퍼셉트론 알고리즘으로 선형 분류 문제를 해결할 수 있음을 증명했다.
  • Perceptron convergence theorem

Perceptron Criterion

---

• 분류를 잘 했다면 아래의 식이 성립한다.
• 예측 값이 양수이면 $y$ 또한 1이고 음수이면 $y$ 값이 -1이기 때문이다.
  $$\bold w ^\top\bold x_n \bold y_n > 0 \ \ \forall \bold x_n$$

object function

• perceptron criterion은 다음과 같은 목적 함수를 유도한다.
  $$\mathcal E(w) = -\sum_{x_n \in \mathcal M}\bold w^\top \bold x_ny_n$$
• 이때 $\mathcal M$은 misclassified된 $\bold x_n$의 set이다.
  • misclassified 되면 $\bold w ^\top\bold x_n \bold y_n$값이 음수이다.
• 즉 위 목적 함수의 값을 최소화하는 것이 학습 목표가 된다.
  • 그레디언트를 구하자.
    $${\partial \mathcal E \over \partial w} = - \sum_{x_n \in \mathcal M} \bold x_n y_n$$

Learning

• 다음과 같이 $w$를 업데이트 할 수 있다.
  $$\Delta \bold w = \alpha \sum_{x_n \in \mathcal M} \bold x_n y_n$$

Algorithm outline

---

1. training sample을 준비한다.
2. misclassified를 찾는다.
   2.1. correctly하면 넘어간다 .
   2.2. incorrectly하면 $w$를 업데이트 한다.
   $\bold w_{k+1} = w_{k} + \alpha \bold x_ny_n$
3. 수렴할 때까지1, 2를 반복한다.

Logistic regression

---

차이점이 뭘까?

• 단일 퍼셉트론은 로지스틱 회귀와 크게 다른 점이 없다.

• 다만 결과에 있어 차이점이 있다.

  • 로지스틱 회귀는 클래스의 확률을 제공한다.
  • 다만 퍼셉트론은 고정된 임계 값을 기준으로 예측 값을 만든다.

Limit

---

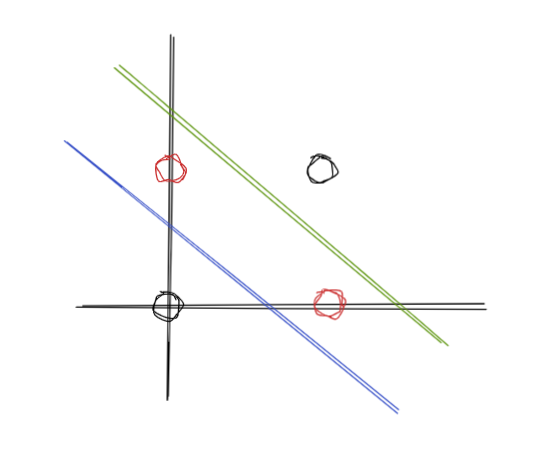
XOR

---

• 만약 데이터가 선형적으로 분류 가능하면 유한한 시도 안에 수렴하는 hyperplane을 구할 수 있다.
• 그러나 선형적으로 분류 가능하지 않은 문제에서는 한계가 있었다.
• 1969년 “Perceptrons:An Introduction to Computational Geometry”, Minsky and Papert 에서 단순한 배타적 논리합 분류 문제를 풀 수 없는 것을 증명했다.
• 이후 첫 ai winter가 찾아온다…

아래 사진처럼 xor문제를 푸는 초평면을 구할 수 없다.