Regularization

Regularization

Overfitting

---

• 좋은 모델의 조건

  • 학습 데이터를 잘 설명하는 모델
  • 미래 데이터 또한 잘 예측하는 모델

• 만약 위 사진처럼 과적합이 된다면

  • 학습 데이터를 잘 설명하지만 실제 데이터에서는 오차가 증가하게 된다.

• 고로 generalization이 필요하다.

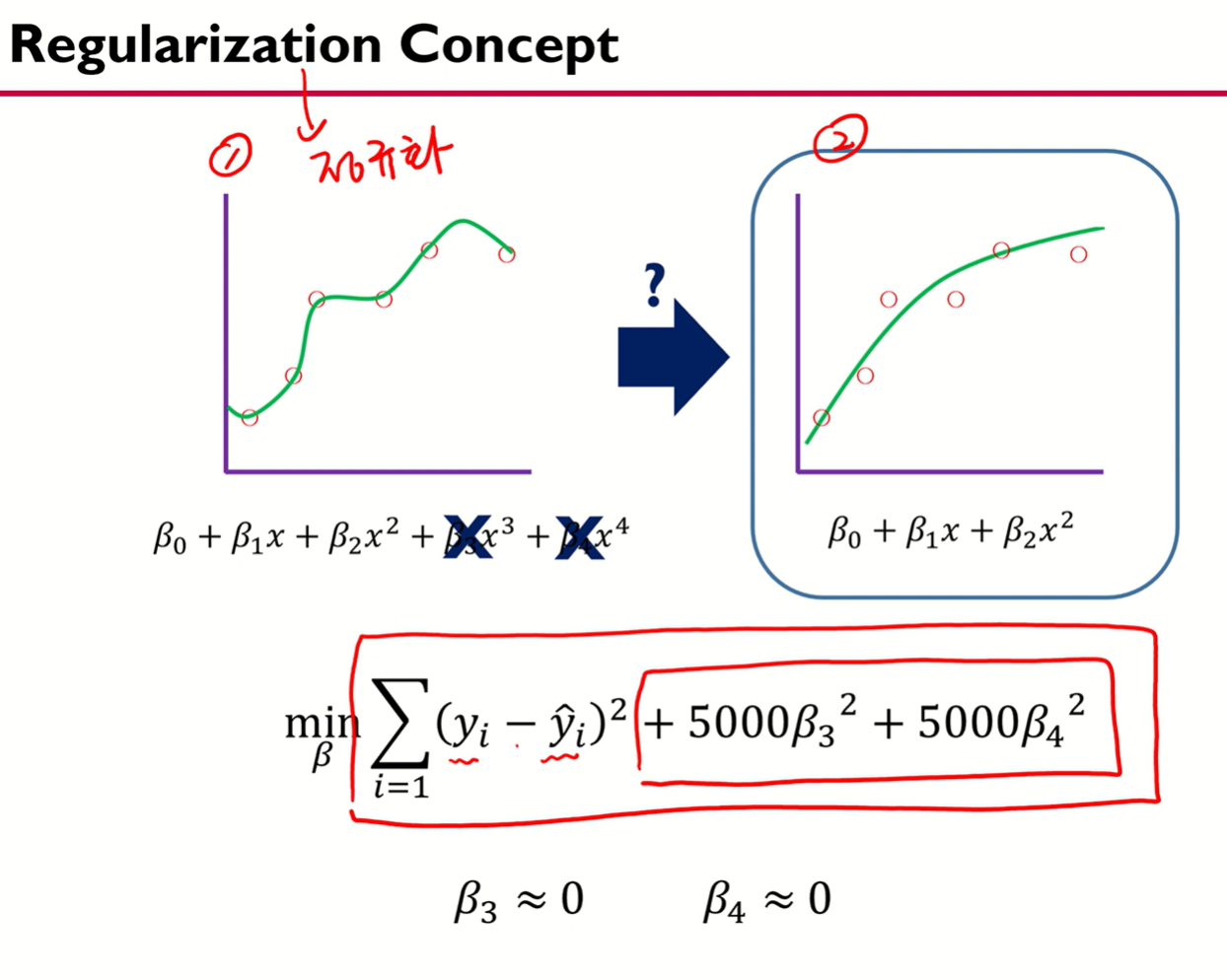
Concept

---

어떻게 규제할 것인가?

• $w$ 값에 제한을 둔다.
  • 일정 크기보다 작게 제한

https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s 출처

이유

• 차수를 낮추는 방법

  • 차수가 높아지면 모델이 오버피팅된다.
  • $w$값을 0으로 근사시켜 차수를 줄인다.
    • 영향력을 줄인다.

• 제한이 없다면 $w$값이 무한히 커질 수 있다.

  • 이는 분산이 커지는 문제가 있다.

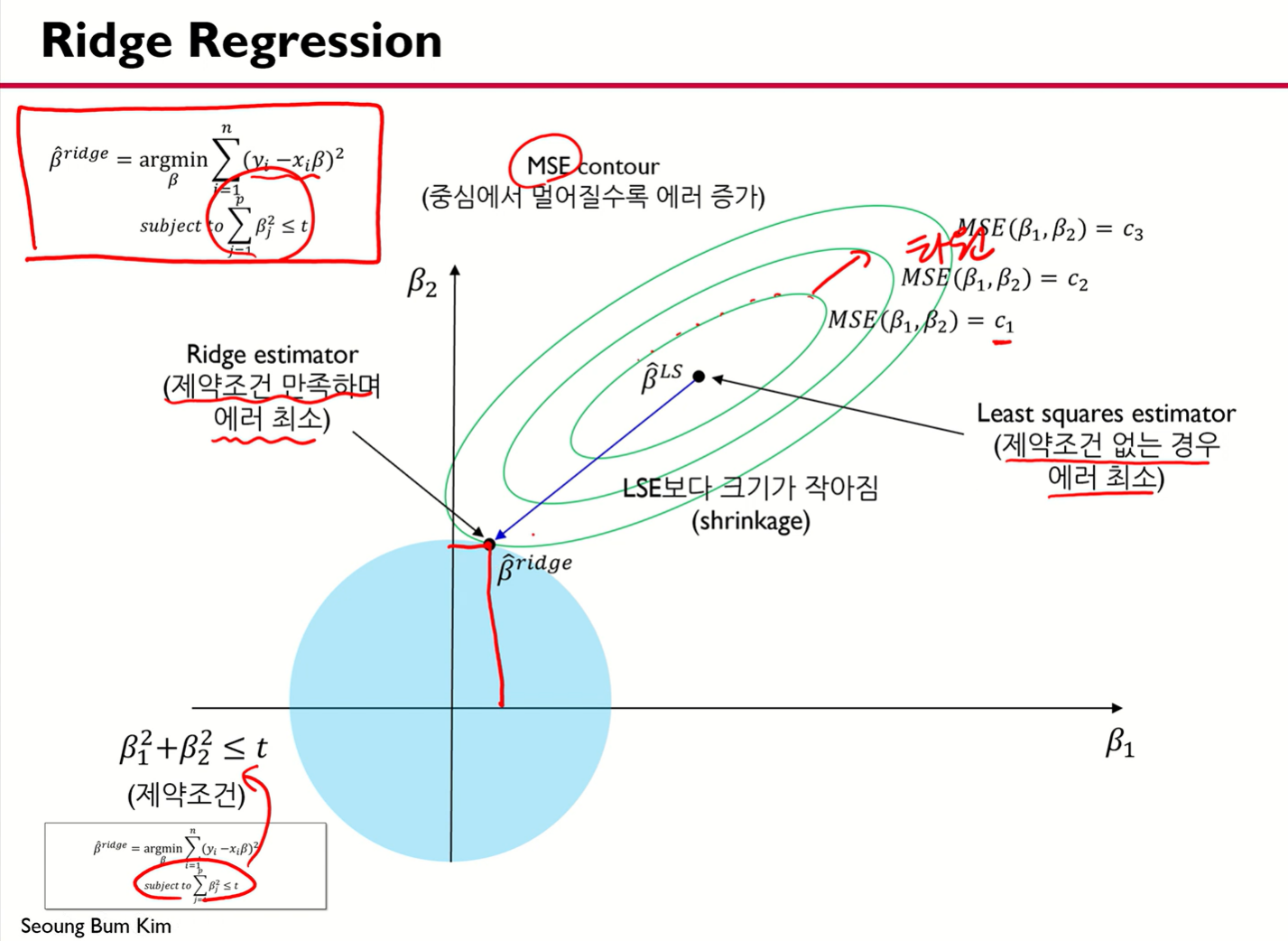
Ridge Regression

---

Form

---

• 릿지는 다음과 같이 $w$를 제한한다.
  • L2 제약이라 부른다 .

$$\min_w {1\over 2}|| \boldsymbol y- \boldsymbol \phi^\top \boldsymbol w||_2^2 \ \text{, \ s.t} \ ||\boldsymbol w||_2^2 \ \le B$$

Sol

---

• 이를 풀어내려면 Lagrange form으로 나타내야 한다.

Lagrange Multiplier Method 는 제약식이 있는 최적화 문제를 푸는 방법이다.
Lagrange Multiplier를 식에 더해 제약이 없는 문제로 바꿀 수 있다.

$$L_p = (\bold y-\boldsymbol \phi^\top \bold w)^\top( \bold y-\boldsymbol \phi ^\top \bold w ) + \lambda(||\bold w||_2^2-B)$$

$L_p$ : Lagrange primal function
$\lambda(||\bold w||_2^2-B)$ : regularizer

• 이제 미분을 해서 $w$값을 구한다.
  • 최소 값을 가지게 만드는 $w$를 찾음

$${ \partial \over \partial w } [(\bold y-\boldsymbol \phi^\top \bold w)^\top( \bold y-\boldsymbol \phi ^\top \bold w ) + \lambda(||\bold w||_2^2-B)] = 0$$

$$w_{LS} = (\boldsymbol \phi\boldsymbol \phi^\top + \lambda I_n ) ^{-1} \boldsymbol \phi \boldsymbol y$$

$I$ : Identity matrix

특징

---

• $\lambda$의 값에 따라 $w$ 값이 변한다.
  • $\lambda$를 shrinkage parameter라고 부른다.
• $\lambda$가 0이면 규제가 없는 상태다.
• $\lambda$가 무한에 가까워지면 $w$값은 0에 근사한다.

https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s

Rasso Regression

Form

---

• 라쏘는 다음과 같이 $w$를 제한한다.
  • L1 제약이라 부른다 .

$$\min_w {1\over 2}|| \boldsymbol y- \boldsymbol \phi^\top \boldsymbol w||_2^2 \ \text{, \ s.t} \ |\boldsymbol w| \ \le B$$

Sol

---

• Lagrange primal function 형태로 나타내자.
  $$L_p = (\bold y-\boldsymbol \phi^\top \bold w)^\top( \bold y-\boldsymbol \phi ^\top \bold w ) + \lambda(|\bold w|-B)$$

$${ \argmin_w} [(\bold y-\boldsymbol \phi^\top \bold w)^\top( \bold y-\boldsymbol \phi ^\top \bold w ) + \lambda(|\bold w|-B)]$$

• $w$의 추청 값을 구하는 정규 방정식은 존재하지 않는다.
  • closed form solution
• $w$ 값이 1이상이면 미분 불가능하다.
  • 0이면 Subgradient 사용 가능

특징

---

• 어떤 관점에서 라쏘는 변수 선택에 사용된다.
  • 선형대수와 ~ 머신러닝 p.184
• 다음 그림에서 보이듯 L1-norm 에서 축이 0이 된다.