RNN-1

딥러닝을 이용한 자연어 처리 입문의 그림을 가져왔다

• 자세한 내용은 위 책을 참고하자.

Sequence Modeling

---

• 목적 : Probability over sequences, x~p(x1, x2, … xT)
• 시계열 데이터 : 시간 순서로 배열된 데이터

Feedforward Net

---

$$\bold{y}_t = \varphi(\bold W_{yh}\bold h_t + \bold b_y)$$

$$\bold{h}_t = \varphi(\bold W_{yh}\bold x_t + \bold b_y)$$

• input data 가 들어올 때마다 독립적이다.

Vanilla RNN

---

$$\bold{y}_t = \varphi(\bold W_{yh}\bold h_t + \bold b_y)$$

$$\bold{h}_t = \varphi(\bold W_{yh}\bold x_t +\bold W_{hh}\bold h_{t-1} + \bold b_y)$$

• 이전 데이터의 h 값을 반영한다.

• 이를 unfolding computational graph로 나타내면 다음과 같다.
  • 은닉층의 노드를 메모리 셀이라 부르기도 한다.

• 이를 그림으로 나타내면 이해가 쉽다.

여러 설계 방식

---

• 용도에 따라 출력과 입력의 길이를 다르게 설계할 수 있다.

• many to many 에서는 Encoder-Decoder 방식도 있다.

Backprop through Time

---

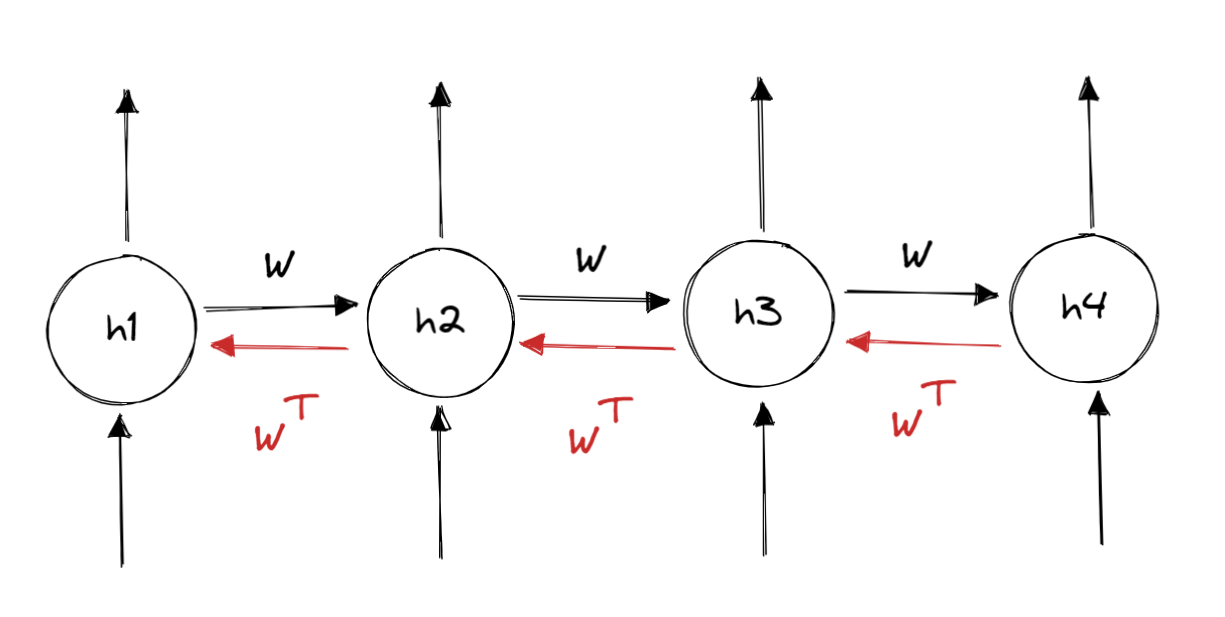
• 그래디언트가 계산될 때는 각 모델의 output에도 영향을 받지만 그 다음 모델의 영향도 받는다.
• feed forward 에서는 w 값이 계속 곱해진다.
• 반대로 backpropagation 과정에서는 $\bold w^T$ 가 곱해진다

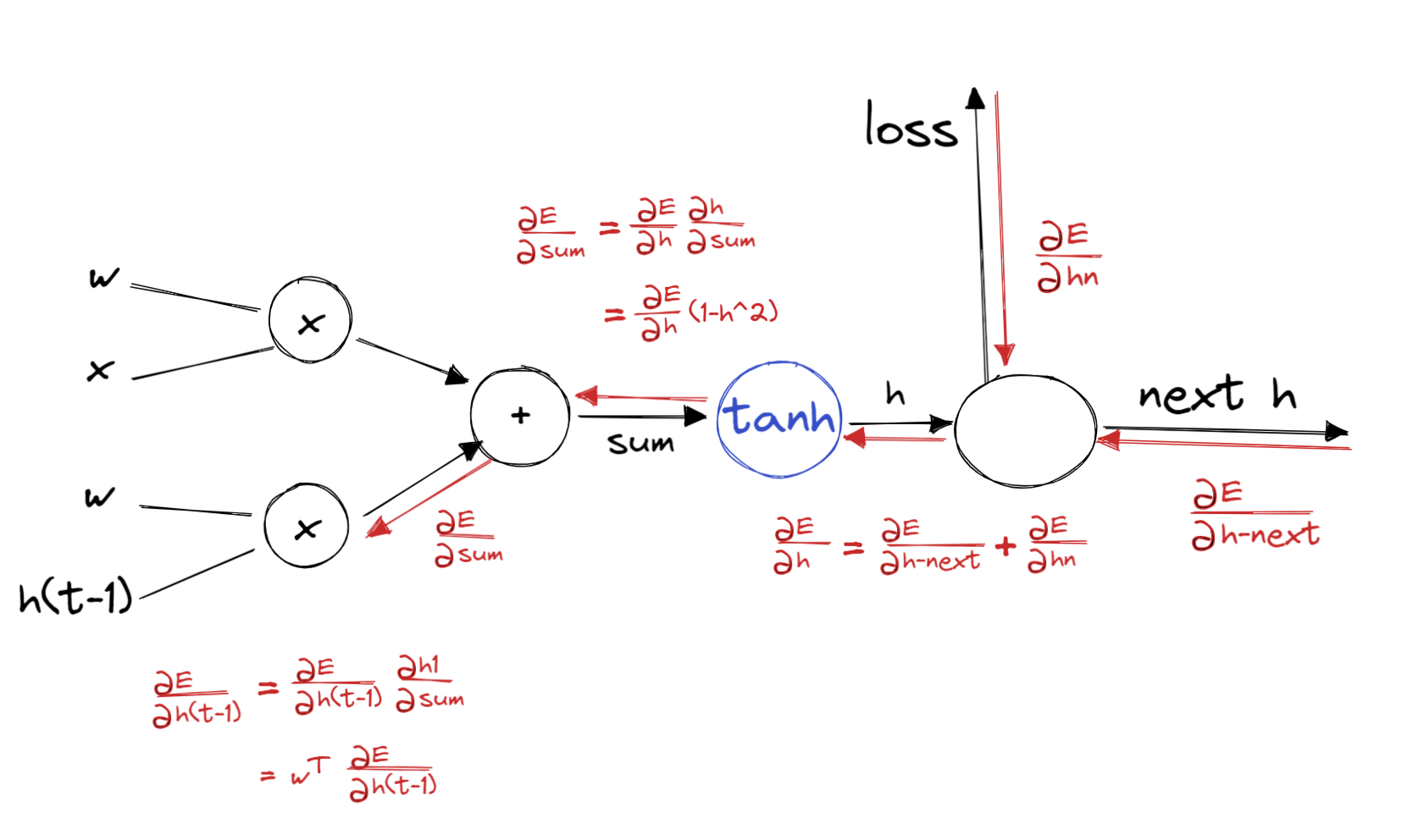
problem

• Exploding gradients
  • when largest singular value > 1
• Vanishing gradients
  • when largest singular value < 1